反向传播(Back Propagation)
通常在设计好一个神经网络后,参数的数量可能会达到百万级别。而我们利用梯度下降去跟新参数的过程如(1)。但是在计算百万级别的参数时,需要一种有效计算梯度的方法,这种方法就是反向传播(简称BP), 因此BP并不是一种新的算法,使用BP就是能够使计算梯度时更加有效率。

其中θ为神经网络的参数,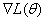 为梯度。
为梯度。
链式法则
设有两个函数为y=g(x),z=h(y),那么要计算z对x导数,则计算过程如(2)

设有三个函数为x=g(s),y=h(s),z=k(x,y),那么要计算z对x导数,则计算过程如(3)

BP计算过程
假定我们设计的神经网络结构如图1-1所示,其中yj神经网络为输出值,dh为隐藏层神经元的输出值,xi为输入值,bj、mh分别是隐藏层和输出层神经元的偏置;
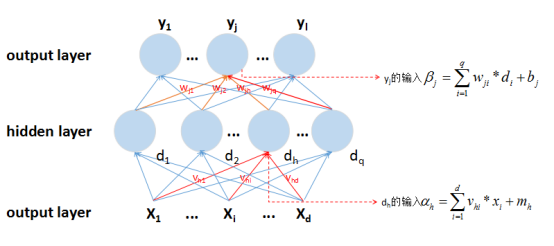
图1-1 神经网络结构
设神经网络的损失函数为L(θ)(L(θ)具体的结构根据实际情况来确定,θ表示所有参数);wjh的更新形式为

由于wjh是通过影响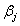 ,继而影响yj,最终影响L(θ)。因此wjh的更新计算可以通过(2)的链式法则进行展开。
,继而影响yj,最终影响L(θ)。因此wjh的更新计算可以通过(2)的链式法则进行展开。

其中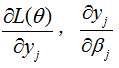 ,需要在确定激活函数和损失函数的具体结果后才就可以进行微分。而
,需要在确定激活函数和损失函数的具体结果后才就可以进行微分。而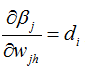 则可以在神经网络前向传播的过程中就可以计算,因此这一项的计算是自下向上,因此也称作forward pass。
则可以在神经网络前向传播的过程中就可以计算,因此这一项的计算是自下向上,因此也称作forward pass。
类比于wjh的更新情况,bj的更新计算为

再计算vhi的的更新情况,跟wjh的更新情况没有太大差别。vhi通过影响输入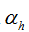 ,继而影响dh,dh通过影响所有的输出层神经元的输入
,继而影响dh,dh通过影响所有的输出层神经元的输入![]() ,继而影响输出值Y={y1,y2,...yl},最终影响L(θ),因此需要运用(3)进行链式法则展开
,继而影响输出值Y={y1,y2,...yl},最终影响L(θ),因此需要运用(3)进行链式法则展开
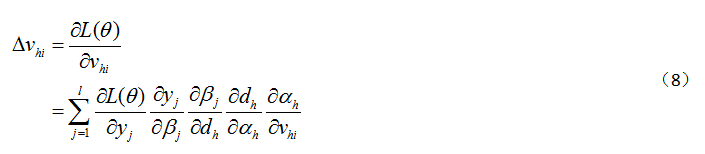
其中(8)中的![]() 跟计算
跟计算 的部分项相同。因此,要计算下层参数的微积分,就需要计算上层参数的微积分。整个参数的更新计算自上向下,这个计算过程也称作backward pass。
的部分项相同。因此,要计算下层参数的微积分,就需要计算上层参数的微积分。整个参数的更新计算自上向下,这个计算过程也称作backward pass。
参考资料
[2]《机器学习》-周志华